Coding

In general, this implementation of merge-sort was written with the goals of reducing the size and complexity of the code, and delaying measurement related i/o until a process had finished its active participation in the sort. Non-blocking send/receive were used where possible, to increase the amount of processing that could be done concurrently. Particular success was achieved in reducing the number of mathematical operations necessary, compared with the initial straightforward code. The most significant improvement of this type was in the merge algorithm. The basic algorithm involves taking two sorted arrays, comparing their first elements, and adding the smaller one to the beginning of the merged array. This comparison and adding is continued until there are no elements left in either source array. The most straight forward implementation uses a loop from 0 to (source array size 1) + (source array size 2). If you've reached the end of array 1, just add the rest of array 2, if you've reached the end of array 2 just add the rest of array 1, and if you haven't reached the end of either, add the smaller of the numbers at the heads of the source arrays, and increment the index that defines the heads of both source and destination arrays. Here is some C code to demonstrate:

intd1=0, d2=0, m=0;


for (m=0; m<(data_size1+data_size2); m++)

{


if (d2>=data_size2)


merged[m]=data1[d1++];


else if (d1>=data_size1)


merged[m]=data2[d2++];


else if (data1[d1]<data2[d2])


merged[m]=data1[d1++];


else


merged[m]=data2[d2++];

}

The debug build for the above code, using Visual C++, executes 51 lines of code for each loop, on average. This number can be used as a rough indicator of expected computation time. The complexity of this implementation of merge is O(n), so the time it takes to perform a merge is proportional to the size of the arrays to merge and the number of CPU cycles per loop. If the amount of processing done for each loop can be reduced, computation time should improve. Much of the end of array checking, which adds up to thousands of comparisons, can be avoided. We can say with absolute certainty that the least number of loops it could take for one source array to run out of elements corresponds to the case where only elements from the smaller array are used until there are no more elements in that array. It may take many more than this minimum number of loops before one of the source arrays runs out of elements to add to the destination array, but there is no quick way to predict that. While both source arrays have elements left, we can easily determine which array is smaller. Knowing the number of elements in the smaller source array, it is safe to perform a merge loop for at least that many cycles without checking for end of array. The following code implements this improvement:

int d1=0 d2=0, m=0,smaller;


while((d2<data_size2)&&(d1<data_size1))

{  // calculate the number of elements we can merge without 
// testing for the end of arrays data1 or data2.




smaller = (data_size1-d1)<(data_size2-d2)?data_size1-d1:data_size2-d2;


smaller += m;

// we can safely do smaller loops w/o error checking - 
// should cover 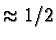$\approx{1/2}$
of remaining data in each pass


for (; m<smaller; m++)


merged[m] = data1[d1]<data2[d2] ? data1[d1++] : data2[d2++];

}

Once the end of one of the arrays is reached, start another loop that just adds the remaining elements to the end of the destination array, as in the next section of code:

smaller = data_size1+data_size2;

// one array is done, finish with the rest of the other array


if (d2>=data_size2)


for(;m<smaller; m++)


merged[m]=data1[d1++];


else


for(;m<smaller; m++)


merged[m]=data2[d2++];

Compared to the first sort implementation, trials with a Visual C++ release build, run on the same 3000 arrays of 50,000 random integers each, show a speed improvement of 11.8% in sort time, and 1.9% overall for all processes time on one node. The number of instructions in an average loop, for a debug build with Visual C++, is reduced from 51 to 33, with an additional 24 instructions each time it is necessary to check for the size of the smaller array. The portion of the loop which is executed for every element added to the destination array has complexity O(n). The 24 instruction section which checks for the end of either source array is O(ln(n)), so it disappears relative to the O(n) part as n increases.
Both of the above implementations of merge can execute much faster if the end of one of the arrays is reached early in the process. This is most likely to happen either if one array is much shorter than the other, or if one array has lower numbers than the other. Neither situation is likely to apply for merge sort. The merged arrays result from dividing larger arrays in half, so their size will differ by at most one element. Since the data is random, it is unlikely that the content of the arrays will be different enough that one will have all its elements merged into the destination array long before the other.
For merging arrays of similar size and content, and knowing that the rand() function generating the numbers returns unsigned integers less than 32768, an even faster and very simple merge algorithm is possible. If we expected one array to run out of numbers faster than the other, the previous implementations might be faster since they take advantage of that possibility. But when the size and content of the arrays to be merged are very close, we can expect to reach the end of each array at about the same time. Since the int type can hold numbers larger than those returned by rand(), we can avoid checking for the end of the source arrays altogether by simply allocating an extra array member, and putting a number 32768 or larger as the last member of the array, after the actual data. When an array runs out of actual data, the next number from that array will always be higher than the remaining actual data in the other array. Merging from that array is effectively blocked. From that point, execution could be faster by detecting the end of one array. But the end of array checking code slows down execution enough when both arrays have data that there is a net benefit to leaving it out. We know the size of the merged array, so we stop looping when that number is reached. The implementation follows:

voidmerge1(int * data1, int data_size1, int * data2, int data_size2, int * merged)

{


int d1=0, d2=0, m, total;


total = data_size1 + data_size2;

// expect to find a large number at the end, so don't 
// check for the end using array size


for (m = 0; m<total; m++)


merged[m] = data1[d1]<data2[d2] ? data1[d1++] : data2[d2++];

}

The above code compiles to 34 instructions with a Visual C++ debug build. While all of the above sections of code have time complexity O(n), so execution time scales linearly with array size, each performs a different number of steps per array element. This third implementation of merge performs 38.4% faster than the first implementation, comparing Visual C++ release builds on the same set of 3000 50,000 element arrays of pseudo-random integers. Figure 7 shows the results of all 3000 test runs. One interesting property of the last implementation of merge is that the variance of execution times is much less than with the other implementations. This is most likely because with no end of array checking, the same number of loops is executed for each run.

  

Figure 7: Comparison of execution times of a single function with 50,000 integers for three merge algorithms.