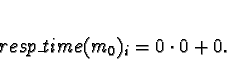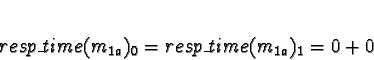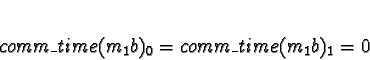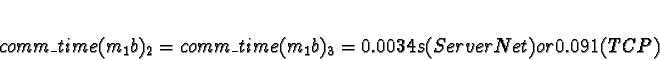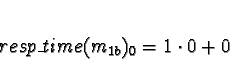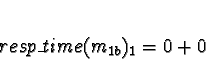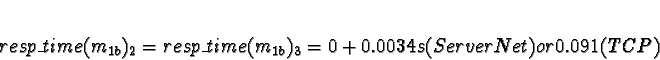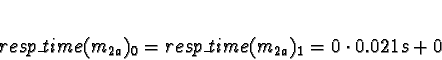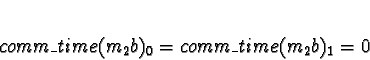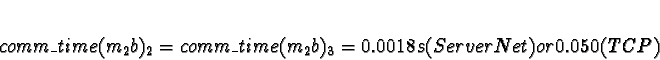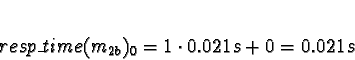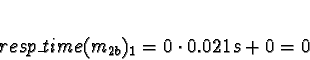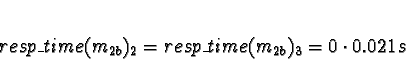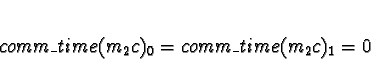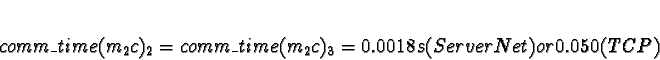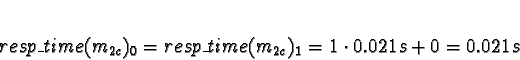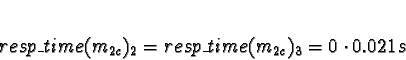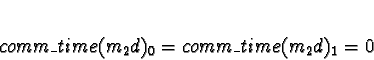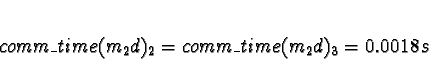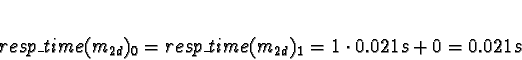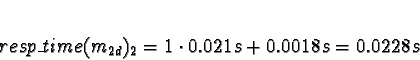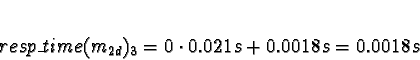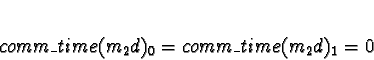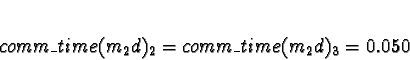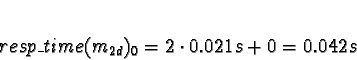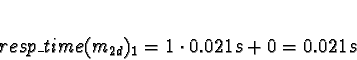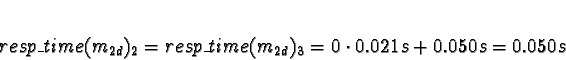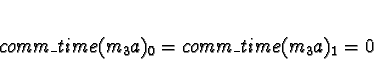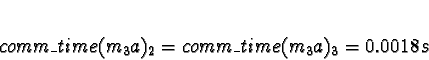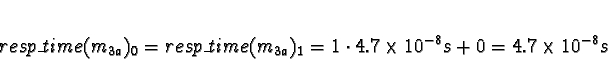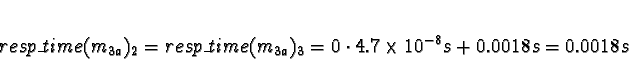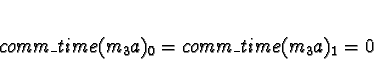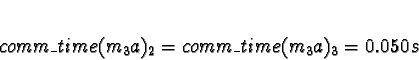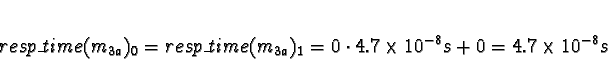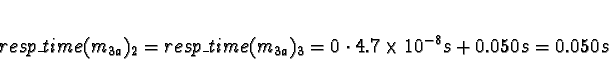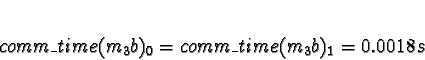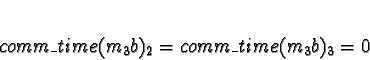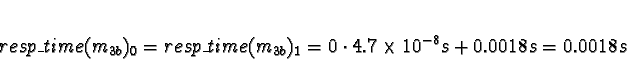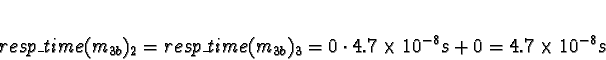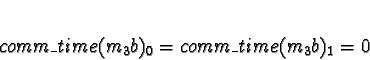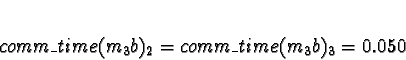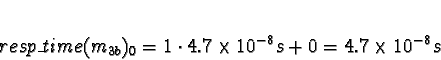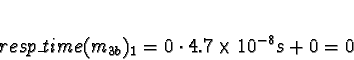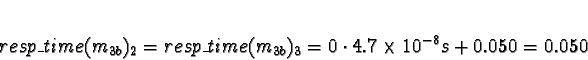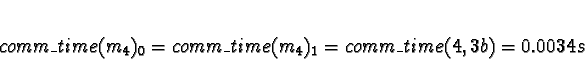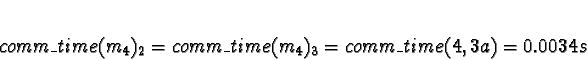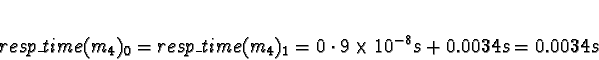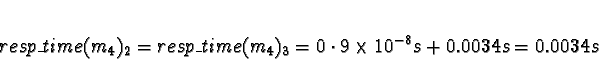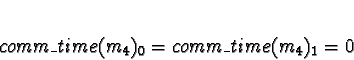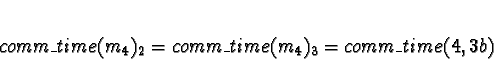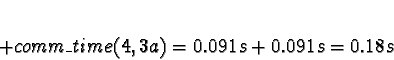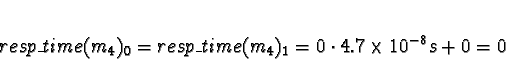


Next: Experimental Results
Up: Parallel Processing and Process
Previous: Parallel Processing and Process
Figure 8:
Application Graph showing processing nodes and data flow relationships for merge-sort.
|
|
The application graph describing processing and data flow for the
three level tree used in this merge-sort implementation is shown in
Figure 8. The numbers appearing in each circle are the
task numbers used to refer to each task in calculations, and next to
each arrow is the number of Bytes passed from one task to the next.
Processors are numbered as follows: 0 and 1 are on machine 0, and 2
and 3 are on machine 1. Estimates for data latencies are based on
throughput tests which measured the time to pass arrays of various
sizes over each of the system interconnects considered. Computation
time was estimated as the average for 1000 test arrays run on a single
workstation and measuring the execution time for the sections in
question. The non-blocking send and receive calls used take a
negligible amount of time to set up the DMA transfers required, so
their execution time is estimated as 0. The algorithm starts with
task 0, and when two tasks are ready for allocation at the same time,
their allocations are calculated from left to right as they appear in
the application graph.
Task 0
No other tasks are allocated, so
All choices are equal, so arbitrarily pick processor 0.
Tasks 1
Task 1a is allocated when task 0 is exiting, so don't consider task 0
to compete for processor time. Di is 0 for all processors.
No times will be less than 0, so allocate 1a to processor 0.
When allocating task 1b, task 1a must be considered allocated.
D0 = 1
D1 = D2 = D3 = 0
Processors 0 and 1 are effectively the same, but pick 1 since it's
slightly more legitimately 0 than processor 0 is. In practice, this has
no effect on the experimental results since it is left to WindowsNT to allocate
processors on the same machine.
Tasks 2
Tasks 2a-2d perform most of the processing, and it is estimated that
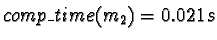 ,
which is a fourth of the time the sort
took when executed as a single process.
2a is in the same situation 1a was, where all predecessors are done
execution and about to pass data.
,
which is a fourth of the time the sort
took when executed as a single process.
2a is in the same situation 1a was, where all predecessors are done
execution and about to pass data.
No times will be less, so allocate 2a to processor 0.
Task 2b is in a similar situation to 1b, except the data passing delay
is approximately half and processor 0 has a measurable work load.
D0 = 1
D1 = D2 = D3 = 0
+ 0.0018s (ServerNet) or 0.050 (TCP) = 0.0018s (ServerNet) or 0.050 (TCP)
Processor 1 clearly has the minimum response time.
Task 2c now has to consider 2 other processes contending for processor
time.
D0 = D1 = 1
D2 = D3 = 0
+ 0.0018s (ServerNet) or 0.050 (TCP) = 0.0018s (ServerNet) or 0.050 (TCP)
Here the calculations have gotten interesting. We see that if the network is TCP/IP, using processors 2 or 3 would give a response time of 0.050s, which is slower than the 0.021s from allocating the task to processors 0 or 1. Pick 0.
If the network is ServerNet, on the other hand, using processors 2 or 3 would give a response time of 0.0018s, which is faster than the 0.021s from allocating the task to processors 0 or 1. Pick 2.
Task 2d is much the same as 2c.
If using ServerNet:
D0 = D1 = D2 = 1
D3 = 0
Pick 3.
If using TCP/IP:
D0 = 2
D1 = 1
D2 = D3 = 0
Pick 1. Knowing that the computation time for tasks 3 and 4 is several orders of magnitude less than the communication time it would take to send the data over 10BaseT Ethernet using TCP/IP, it should be obvious at this point that no tasks will be sent to the other workstation.
Tasks 3
Task 3a is preceded by tasks 2a and 2b, so allocation takes place when
both have completed. If using ServerNet, 2c and 2d are expected to still be
executing on processors 2 and 3.
With ServerNet:
D0 = D1 = 0
D2 = D3 = 1
Pick processor 0.
With TCP/IP:
D0 = D1 = D2 = D3 = 0
Pick processor 0.
Task 3b is preceded by 2c and 2d, which are expected to finish after
3a for ServerNet, so all processors are available. With ServerNet:
D0 = D1 = D2 = D3 = 0
Pick processor 2.
For TCP/IP, 3b will be allocated immediately after 3a. With TCP/IP:
D0 = 1
D1 = D2 = D3 = 0
Pick processor 1.
Task 4
At this point, the problem in the ServerNet case is symmetrical with respect
to data passing between workstations.
D0 = D1 = D2 = D3 = 0
All processors look the same. In the implementation, the same process
handles tasks 0 and 4, so task 4 is effectively assigned to processor 0.
In the TCP/IP case, the choice is obvious.
D0 = D1 = D2 = D3 = 0
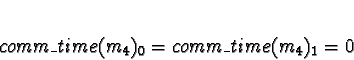
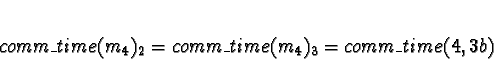
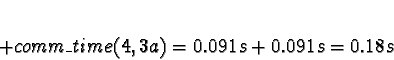
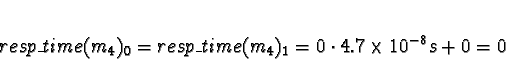
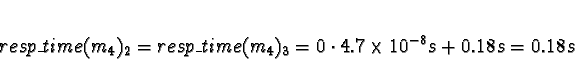
Process 4 should be allocated to processor 0 or 1.
Since there is not a one to one mapping of tasks to processes, in the
case of ServerNet the algorithm doesn't clearly resolve whether the
process responsible for tasks 1b and 3b should go to workstation 0 or
1. Experiments on our system showed that these two arrangements in
fact perform very similarly. Allocating it to workstation 1 performs
slightly better, which is likely due to there being less overhead for
sending data as one chunk instead of two.
Using the idea that total execution time is the same as the longest
execution path, it is possible to calculate an expected execution time
for our system using ServerNet or TCP/IP. For ServerNet, the longest execution
path follows task 0-1b-2d-3b-4. The sum of execution times and data
transmission times is:
0.0018s + 0.021s + 0.0034 = 0.0262s. For TCP/IP the longest path is the same, and the sum is:
0.021s (waiting for a processor) + 0.021 = 0.042. If the ServerNet
process allocation were followed with TCP/IP, the longest path would
be the same, but the expected execution time would be:
0.050s +
0.025s + 0.091s = 0.166, or four times as long as the predicted time
for leaving all processes on one node.



Next: Experimental Results
Up: Parallel Processing and Process
Previous: Parallel Processing and Process
Garth Brown
2001-01-26
![\includegraphics[scale=0.4]{SortAppGraph.eps}](img21.gif)