Description of the Algorithm

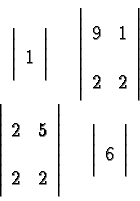
Quadtree matrix data compression involves mapping data to a tree that has a root above four nodes, and each of those is above four nodes, and so on. The general algorithm starts by recursively dividing an array into four equal sub-arrays. Each sub-array is passed to the next layer down in the tree, divided in four parts, and so on until it is divided into four element arrays, as in the following diagram.

$$\left\vert \begin{array}{c\vert c} \left\vert \begin{array}{c... ... \\ 6 & 6 \\ \end{array} \right\vert \end{array} \right\vert$$

At the lowest level, if all four elements are the same, they are compressed into one element, otherwise they are left uncompressed. Either way, the array is passed back to the next level up. At each level of the tree, the sub-arrays passed back are compared. If they are all identical and composed of exactly one element (sub-arrays fully compressed to one are represented as one element), then the four sub-arrays are compressed to one element representing all elements from that point down in the tree.

$$\begin{array}{cc} \left\vert \begin{array}{c} 1 \end{array} ... ...ft\vert \begin{array}{c} 6 \end{array} \right\vert \end{array}$$

Compressed or not, the sub-array is then passed back up the tree all the way back to the root, and tested for compressibility at each level. Partly compressible data will be represented as a combination of elements compressed to different degrees. Internally, data is represented as a size and a value. For instance, the four ones in the example, are represented as 1:1, 1:1, 1:1, 1:1 before compression, and 4:1 after.

$$\left\vert \begin{array}{cc} \begin{array}{c} 1 \end{array}&... ...{array}& \begin{array}{c} 6 \end{array}\end{array} \right\vert$$