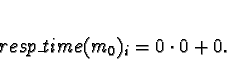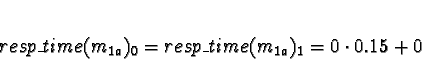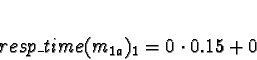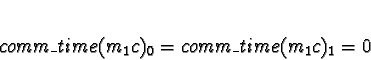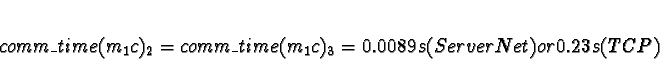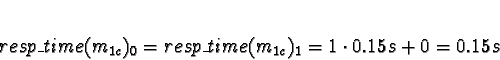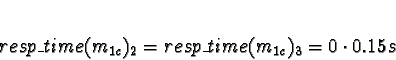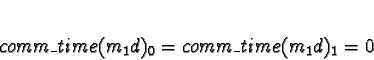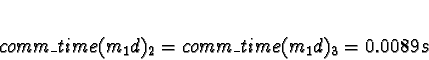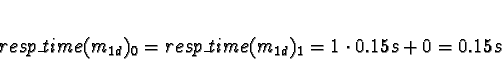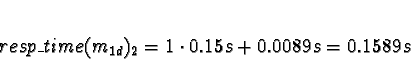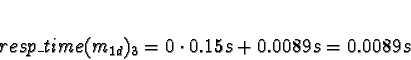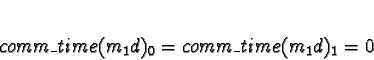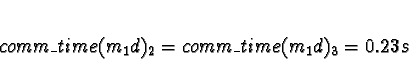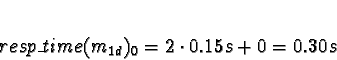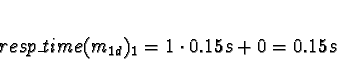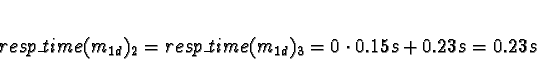


Next: Experimental Results
Up: Parallel Processing and Process
Previous: Parallel Processing and Process
Figure 18:
Application Graph showing processing nodes and data flow
relationships for Quadtree Compression.
|
|
The application graph describing processing and data flow for the
two level tree used in this quadtree compression implementation is shown in
Figure 18. Since the tree only has one level, all
communication is with the same amount of data. For the 256x256
integer arrays used for testing communication will consist of 131,072
Bytes. Processing time for leaf nodes is estimated to be 0.15s, and
processing time at the end for task 2 is estimated to be 0.05s. As
with the merge-sort algorithm, task allocation begins with arbitrarily
picking a processor for the root.
Task 0
No other tasks are allocated, so
All choices are equal, so arbitrarily pick processor 0.
Tasks 1
Task 1a is allocated when task 0 is exiting, so don't consider task 0
to compete for processor time.
D0 = D1 = D2 = D3 = 0
No times will be less than 0, so allocate 1a to processor 0.
Task 1b
D0 = 1
D1 = D2 = D3 = 0
No times will be less than 0, so allocate 1b to processor 1.
Now for task 1c.
D0 = D1 = 1
D2 = D3 = 0
+ 0.0089s (ServerNet) or 0.23s (TCP) = 0.0089s (ServerNet) or 0.23s (TCP)
The results are much like those for merge-sort. We expect that for
ServerNet task 1c should be allocated to processor 2, and for TCP/IP it
should be allocated to processor 0. However, the numbers for TCP/IP
in quadtree compression are much closer than they were for
merge-sort. Quadtree compression requires more processing time per
Byte passed than sorting did.
Task 1d will be examined in two parts, one for the ServerNet allocation, one
for the TCP/IP allocation. First ServerNet:
D0 = D1 = D2 = 1
D3 = 0
So allocate m1d to 3. Now TCP/IP:
D0 = 2
D1 = 1
D2 = D3 = 0
So m1d is allocated to processor 1.
Predicted processing times are:
For ServerNet,
0.0089s + 0.15s + 0.0089s + 0.05s = 0.22sFor one node (TCP/IP allocation),
0.15s + 0.15s + 0.05s = 0.35sFor TCP/IP with ServerNet allocation,
0.23s + 0.15s + 0.23s + 0.05s =
0.66sSince the data involved in this algorithm gets compressed, possibly
down to two integers, the factors in the above calculations which
account for data passed from the 1 tasks to task 2 can in some cases
disappear. Having fully compressible data would change the expected
ServerNet time to 0.21s, and TCP/IP allocated to both workstations to 0.43s.



Next: Experimental Results
Up: Parallel Processing and Process
Previous: Parallel Processing and Process
Garth Brown
2001-01-26
![\includegraphics[scale=0.4]{QuadAppGraph.eps}](img87.gif)
![\includegraphics[scale=0.4]{QuadAppGraph.eps}](img87.gif)